こんにちは！ベーです。
今回は正負の数の減法（引き算）を扱っていきます。
引き算かー
授業で受けたけど符号が変わってややこしくなるんだよなー
授業を受けた人たちはわかるかもしれませんが、符号を変えていく過程がありますのよね。
結論としては、その変形を覚えれば問題ないです。
ただ、仕組みもしっかり説明したいと思います。
暗記するだけでなく、理由も理解するだけで数学への理解が変わります。
ぜひ、確認をしてください。
【結論】減算のやり方
理由を説明する前に、結論からお伝えしましょう。
減法 やり方
引く数（左側）の符号を変えて加法に変える
例
\((+3)-(+2)=(+3)+(-2)\)
\((+3)-(-2)=(+3)+(+2)\)
結局は加法と同じだね！
そう！結局は加法にするから
減法は一個作業が増えるイメージだね。
手間だと感じてしまうかもしれませんが、一つずつ丁寧にです！
慣れるまでゆっくりやっていきましょう！
減法の仕組み
2つの例を使って仕組みを理解していきましょう。
例１
\((+5)-(+2)\)
簡単だよ！
\(5-2\)だから\(3\)だよね
結果としては合ってるね。
だけど、なぜ
\((+5)+(-2)\)という計算にできるのかな？
ん？どういうこと？
すーやの考え方は
（正の数）ー（正の数）で求められるということだよね。
僕が聞きたいのは
（正の数）＋（負の数）にできる理由だね。
どうやってできるのか。
これは、
・虫食い算
・数直線
この2つで考えていきます。
また数直線出てきますね。。笑
例１解説
\((+5)-(+2)=◻︎\) の \(◻︎\) を求めればいいんですよね。
小学生の頃、虫食い算やりませんでしたか？
虫食いって\(◻︎\)の入った計算のやつ？
そうです！
例えば、\(◻︎+(+2)=(+5)\) の \(◻︎\) に入る数字を求めたいとします。
その場合は、どう計算すればいいでしょうか？
そりゃ\((+2)\)にあといくつあれば\((+5)\)になるかでしょ？
そうだね！
じゃさ、そのあといくつを求める計算式は？
それは、\((+5)\)から\((+2)\)を引けば残りが出るから。。
あ！
そう！
\(◻︎+(+2)=(+5)\) と
\((+5)-(+2)=◻︎\) に
当てはまる\(◻︎\)はどちらも同じなんだ！
このままだとただの穴埋めになってしまいます。
実際に求める計算はどうなるでしょう。
ポイントは数直線です！
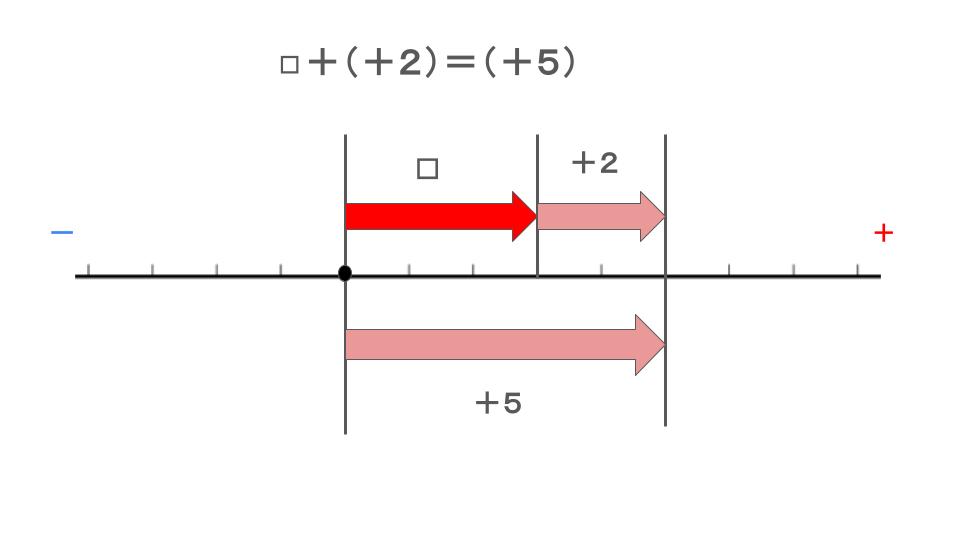
この数直線を見れば、\(◻︎\)に入る数もわかると思います。
これって加法の時にも似たようなことやったな
加法についてはこちらを見てください
さて、\(◻︎\)に入る数を求めるには数直線をこのように見ればいいですね。
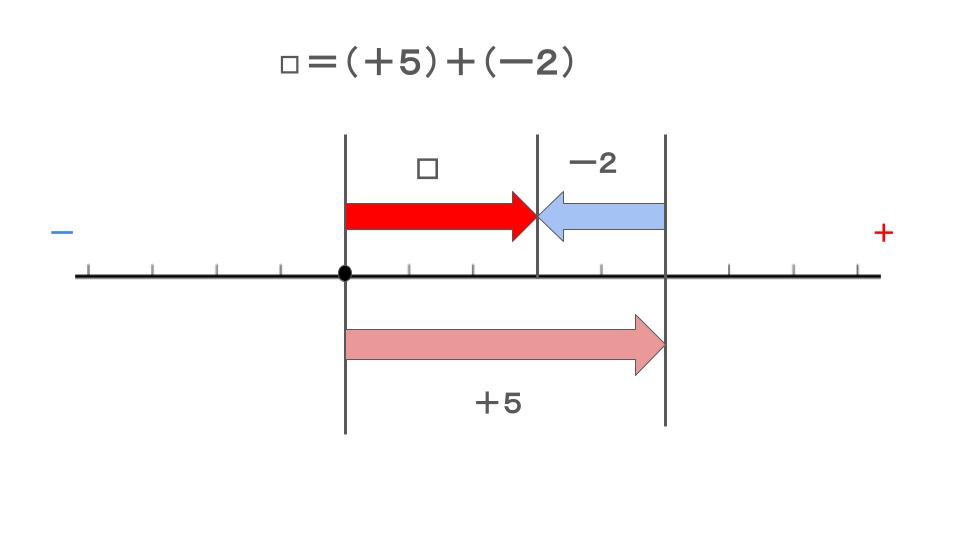
これは加法でもやりましたね。
求める計算式は
\((+5)+(-2)=◻︎\)
になります！
ということは、
\(◻︎+(+2)=(+5)\)の\(◻︎\)を求める式は、
\((+5)-(+2)=◻︎\)でも
\((+5)+(-2)=◻︎\)でも
同じということだね！
そう！
もしよくわからない人は下の図を見てね！
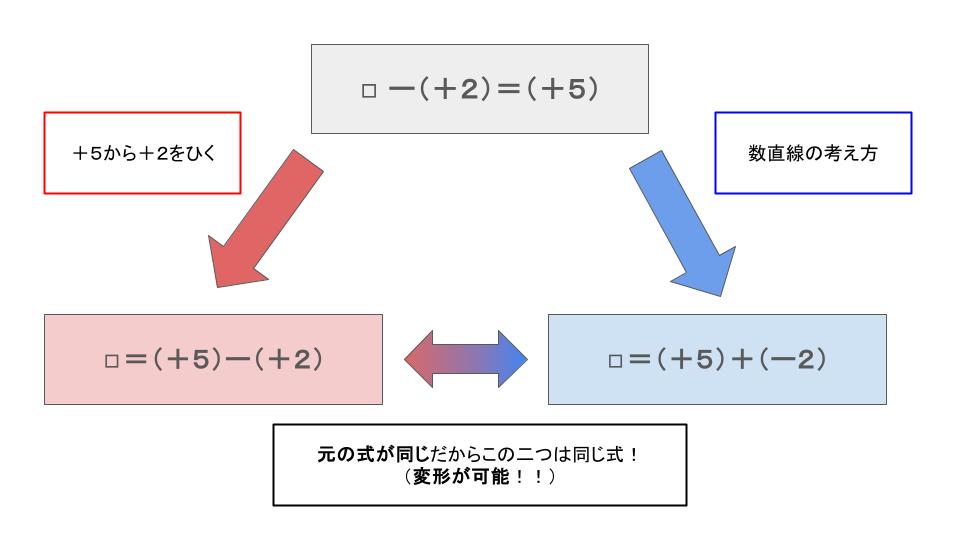
このことから
\((+5)-(+2)=◻︎\)と\((+5)+(-2)=◻︎\)は同じになることがわかります。
改めて減法についてです。
減法 やり方
正負の数の符号を変えて加法に変える
例
\((+3)-(+2)=(+3)+(-2)\)
\((+3)-(-2)=(+3)+(+2)\)
理由はなんとなくわかったよ。
（正の数）ー（負の数）と
（正の数）＋（正の数）
になるものは、同じように考えればいいのかな？
そうだね！
虫食いと数直線を使って考えてみよう！
練習問題
やることは単純なので、仕組みを理解したらあとは演習して覚えてしまいましょう！
問 次の計算をしなさい
(1) \((+5)-(+2)\)
(2) \((+2)-(-5)\)
(3) \((-6)-(+1)\)
(4) \((-14)-0\)
(5) \(0-(-6)\)
(6) \((+1.5)-(+2.4)\)
(7) \((+\frac{1}{12})-(-\frac{5}{12})\)
(8) \((+3)-(+\frac{1}{2})\)
練習問題 解答
解答
(1) \(+3\)
(2) \(+7\)
(3) \(-7\)
(4) \(-14\)
(5) \(+6\)
(6) \(-0.9\)
(7) \(+\frac{1}{2}\)
(8) \(+\frac{5}{2}\)
各計算を以下に書いておきます。
参考にしてください！
(1)
\(\begin{align}
(+5)-(+2) &= (+5)+(-2) \\
&= +(5-2) \\
&= +3
\end{align}\)
(2)
\(\begin{align}
(+2)-(-5) &= (+2)+(+5) \\
&= +7
\end{align}\)
(3)
\(\begin{align}
(-6)-(+1) &= (-6)+(-1) \\
&= -(6+1) \\
&= -7
\end{align}\)
(4)
\((-14)-0 = -14\)
※0を引いても答えは変わりません！出たらラッキー問題！
(5)
\(\begin{align}
0-(-6) &= 0+(+6) \\
&= +6
\end{align}\)
※引く数（左側）が\(0\)でないときは普通の計算と同じようにやります！
(6)
\(\begin{align}
(+1.5)-(+2.4) &= (+1.5)+(-2.4) \\
&= -(2.4-1.5) \\
&= -0.9
\end{align}\)
(7)
\(\begin{align}
(+\frac{1}{12})-(-\frac{5}{12}) &= (+\frac{1}{12})+(+\frac{5}{12}) \\
&= +(\frac{1}{12}+\frac{5}{12}) \\
&= +\frac{6}{12} \\
&= +\frac{1}{2}
\end{align}\)
※約分忘れずに！
(8)
\(\begin{align}
(+3)-(+\frac{1}{2}) &= (+3)+(-\frac{1}{2}) \\
&= +(\frac{6}{2})+(-\frac{1}{2}) \\
&= +(\frac{6}{2}-\frac{1}{2}) \\
&= +\frac{5}{2}
\end{align}\)
※通分をして、加法を行う。
以前やったことですね！
まとめ（左側の符号を変えて加法にする！）
いかがでしたか？
やっていることはシンプルですね。
符号を変えて足すだね！
そうです！シンプルですね。
ただ、その理由を知っておくことが必要です！
しっかりと学習をして、演習を重ねて知識を身につけていきましょう！
それでは！
コメント