こんにちは、ベーです!
今回は、中1になってすぐに、そして長いことお世話になっていく正負の数について考えます!
人によっては
見たことあるし、簡単だよ
だったり
分数、小数ですら無理なのに、ー(マイナス)がつくなんて。。
と色々あると思います。
ですが!大事なのは、+(プラス)やー(マイナス)の表す意味です。
今回は正負の数が何を意味するかを理解できればOKです。
むしろ、この意味を理解せずに、新しい数のように扱っていく生徒が多いですが、
それではこの先の計算で「???」になってしまうでしょう。
今回は
・正負の数の意味を確認したい。
・「ー」がよくわからなくなってしまった。
という人はぜひ確認してください。
雑に流すことなく、そして怯えることなく意味を探っていきましょう!
負の数とは?

負の数というのは
ー3のように、ー(マイナス)がついた数のことを示すよ。
例
負の数・・・\(-3, -1.1, -\frac{1}{5}\)など
授業では、
正の数・・・\(+3, +1.1, +\frac{1}{5}\)など
+(プラス)のついた数 または 0以外の何もついていない数(3, 1.1, \(\frac{1}{5}\)など)
と合わせて+かーがついた数として扱っていますね。

そんなの見たらわかっとるわ!
気温とか、ゲームで見る借金に出てくるやつでしょ?
そう、新しいもののように習っていますが、実は見たことがあるんですよね。

僕が授業をしていた時も負の数を確認すると
気温、ゲームのデバフ(マイナスの効果)
の意見が多かったね。
実際、負の数は中学での数学で扱っていきます。
(小学校の先生によっては予習的な形で習っている人もいるでしょう。)
ここで疑問に思って欲しいのは、、

じゃあ、負の数から習っていく理由はなんだろう?

そんなのわかんないよ!
言われたからそーなんだでやってるだけだし、、
そうなんです。生徒は言われたことをやってるだけですよね。
そりゃ、授業するのは先生だし、先生も扱う内容は決まっているので、、、
ただ、これがあるから「やらされている」・「つまらない」になるわけで、、

それだとこの先、計算で躓いてしまうよ。
今回は負の数を扱う意味と少し問題も扱うよ!
最初に負の数を扱う意味
最初に負の数を扱う意味、それは
・数の範囲が広がっていくことを体験する。
・基準を理解し、今後の計算の土台になる。

数の範囲?基準?
一つずつ説明しますね。
数の範囲が広がっていくことを体験する。
実は小学校でも経験ありますよね?数の種類が増えていったことが、、

整数から、分数や小数になった!
(分数苦手だったな・・・)

だね!ではなぜ、分数や小数が必要になったの?
これもただ習っただけと思わず、必要になった理由を考えてみましょう。
整数だけだと表現できない計算がありましたよね?

整数だけだと、割り算の答えがあまりなしで出せなかったような、
そうです!小学校は「あまり」の考えがありつつも、あまりなしの出し方だと分数、
小数に頼るしかないのです。
あまりの3枚
例 あまりあり(整数だけで表現する場合)
\( 7 \div 4 = 1\) あまり \(3\)
あまりなし(整数以外も使って表現する場合)

\( 7 \div 4 = \frac{7}{4}\)
( または \(1\frac{3}{4} や 1.75\))
小学校で分数やりましたね、苦手を示す子も多いかったでしょう。
(分数苦手な子は復習しよう!!)
負の数も同じです。

負の数が必要になるのはどんな時?

「\(3-4\)」とか「\(1.2-4.3\)」みたいな、
(小さい数)ー(大きい数)の計算だとー(マイナス)が
必要になるね!
主に引き算で必要になりますよね。
このように、新しい数を習うときは、それが必要になる計算が出ているということです。
こういった、数の種類が増えることは数の範囲が広がると言われます。
数の範囲が広がる・・・数の種類が増えていく
目的:さまざまな計算の解答を出せるようにするため
基準を理解し、今後の計算の土台になる

問題です!負の数と正の数の間にあるものは??

えーと、、、0かな

正解!その間にあるものが基準だよ
0より1大きいから+1、1小さいからー1と基準との大小を表現しているんだ。
正の数(+の数)と負の数(ーの数)の間にある数。これが基準です。
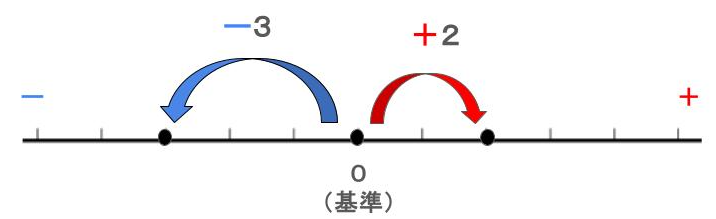
上の図のようにある地点より右に行ったら+、左に行ったらーと表していきます。
(これが計算で活用されます)
すなわち、正の数や負の数は「基準からいくつ、どちら側(+かー)に変化しているか」を示すものになります!
例 3人の平均のお小遣いは月3000円でした。
Aさんは月2000円、Bさんは月3000円、Cさんは月4000円だとします。
このとき、平均のお小遣いを基準としたとき、
Aさんのお小遣いは平均(基準)より1000円少ないので ー1000円
Bさんは平均と変わらないので 0円
Cさんのお小遣いは平均(基準)より1000円多いので +1000円
と表せます。
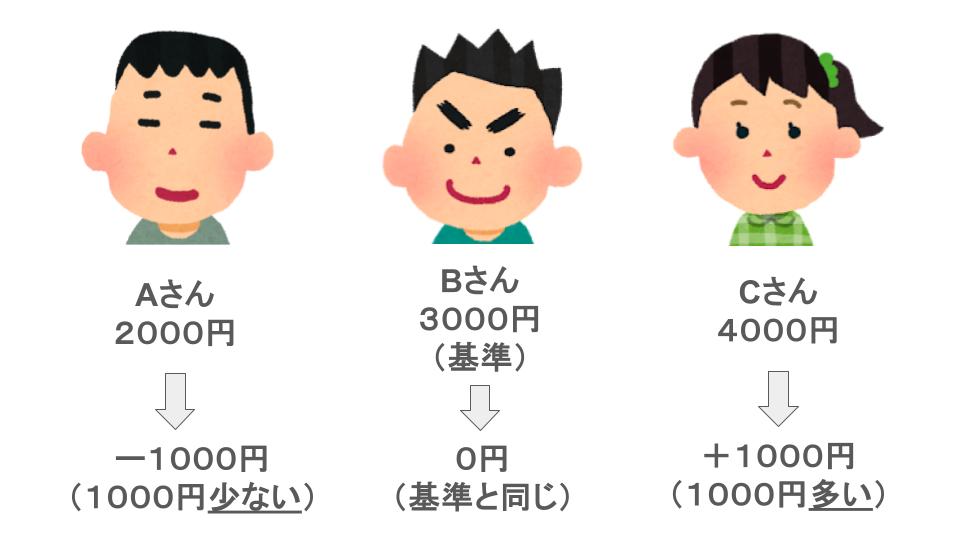
例のように、何を基準として、それより多いのか少ないのかを決める時に+やーは使われます。
基準・・・大小やどのくらい変化したのかの土台になるもの
例、気温:0°、 標高・海面下:海面の高さ、 数直線:0(原点)
練習問題
問1 温度問題

0℃を基準として次の温度を+、ーを使って表しなさい。
(1) 0℃より 4.5℃低い温度
(2) 0℃より 10℃高い温度
※低い・高いを+やーを使って表すことを考えれば簡単ですね。
問2 表から増減を求める問題
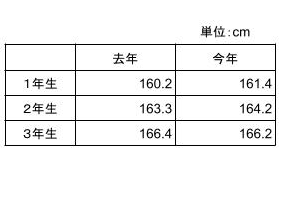
右の表は、ある中学校の各学年の平均身長を表したものである。
去年の人数を基準にして、それより増えたことを正の数、
減ったことを負の数で表すこととする。
(1) 今年の1年生の身長を去年の身長を基準にして、表しなさい。
(2) 今年の3年生の身長を去年の身長を基準にして、表しなさい。
※これが、0以外が基準になるような問題です。
ただ、基準が分かれば、そこからの増加や減少を調べればいいですね!
解答
問1
(1) \(-4.5\)℃
0℃(基準)より、4.5℃低い → ー4.5℃
低いことと、ー(マイナス)を合わせれば答えられますね。
温度を聞かれているので、℃(単位)を忘れずに!
(2) \(+10\)℃
(1)と似たように考えましょう。
0℃(基準)より、10℃高い → +10℃
高いことと、+(プラス)を合わせれば答えられますね。
同様に温度を聞かれているので、℃(単位)を忘れずに!
問2
(1) \(+1.2\)cm

基準が去年の1年生の身長なので、そこからいくつ増えたのか・
減ったのかを調べましょう!
(基準)160.2cm → (今年)161.4cm(1.2cm 増えた)
➡︎ +1.2 cm
(2) \(-0.2\)cm

(1)と同じように考えてみましょう!
基準が去年の3年生の身長なので、そこからいくつ増えたのか・
減ったのかを調べると!
(基準)166.4cm → (今年)166.2cm(0.2cm 減った)
➡︎ ー0.2 cm
まとめ(負の数は基準があってこそ!)

負の数の扱い方や基準について理解できたかな?

基準が何か、そこからどのくらい増減したのかを意識することが大切だね!

そう!増減や移動などの変化した分を表すのが負の数の基本の扱い方だよ。
そこから負の数について調べたり、計算をしていくことになるからね。

うげー。負の数についてはなんとなくわかったけど、ここから大変になってくのか。。。
いかがでしたか?
負の数については直感的にわかることも多いのでスムーズに理解できた人もいると思います。
ただ大切なのは、正負の数が基準からどのくらい変化したのかを示す数だということです!
改めて基準、そして正負の数とは
基準・・・大小やどのくらい変化したのかの土台になるもの
例、気温:0°、 標高・海面下:海面の高さ、 数直線:0(原点)
正負の数・・・基準からの変化の具合を表現する数
これを意識できているか、それとも小学校からの追加でただの数と思っているのかでこの先の理解も変わっていきます。
ぜひ、これを忘れずに忘れたら戻って確認していきましょう!
それでは!



コメント