こんにちは!ベーです。
今回から、掛け算(乗法)に入っていきます。

掛け算かー
法則がわかればいいって習ったな。

もちろん、ここにも法則はあるね!
ただ、なぜそうなるのかを理解するようにしよう。
毎度のように法則はありますが、「なぜそうなるのか」を学んでいきましょう。
・乗法のやり方を確認したい人
・乗法の符号の法則について理解したい人
・なぜ、符号の決まりがあるかを知りたい人
はぜひチェックしください!
乗法の法則
まずは結論からです!
2つの数の場合を確認しましょう。
2つの正負の数の乗法
①同符号の数
➡︎絶対値の積に正の符号(+)をつける。
②異符号の数
➡︎絶対値の積に負の符号(ー)をつける。
絶対値については以下を確認して下さい。

同符号か異符号かを確認すればいいんだね!
そうです。加法の時と同じように符号の組み合わせで求めればいいでしょう。
加法についてはこちらで確認して下さい。

じゃあなぜ、同符号は+で異符号はーなんだろう?

それは、、
授業で言われたから??
それでは、覚えるだけで大変になってしまいます。
なぜそうなっているのかを理解するようにしましょう。
乗法の仕組み(同符号)
(+)✖️(+)=(+)

これはわかるよ!
小学校でやったからね。
こちらは問題ないでしょう。
小学校で掛け算をやったように、ただの数字は正の数と見ることができますね。
今後のパターンのために、1つの例と図を使って確認します。
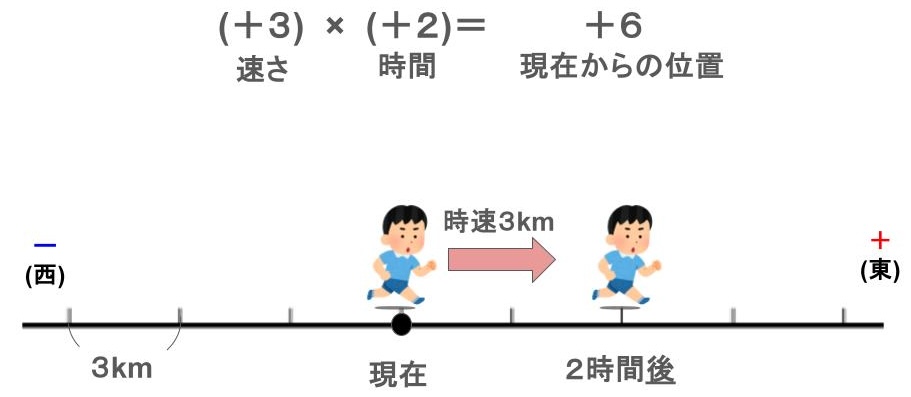
例 \((+3)\times(+2)\)の計算

答えは\(+6\)だよ。簡単だね。
答えは簡単ですが、求め方を次のようにします。
かける数(左の数)を時速、かけられる数(右の数)を時間として
移動距離を求める計算をします。
例の場合
東の方向に時速3kmで歩いた時、2時間後の位置
答え 東に6km移動した場所
※時速は+を東の方向、ーを西の方向とし
時間は+を後の時間、ーを前の時間とします。

速さ、時間、距離。。?
速さについて簡単に確認します。
わからない人は確認して下さいね。
何度も覚えられない人は最後のコラムをみて下さい!
速さ・時間・距離の関係
(距離)=(速さ)\(\times\)(時間)
(速さ)=(距離)\(\div\)(時間)
(時間)=(距離)\(\div\)(速さ)
(ー)✖️(ー)=(+)

これは、式だけ見てもよくわからないんだよね。。

同じように例と図を使って考えていくよ!
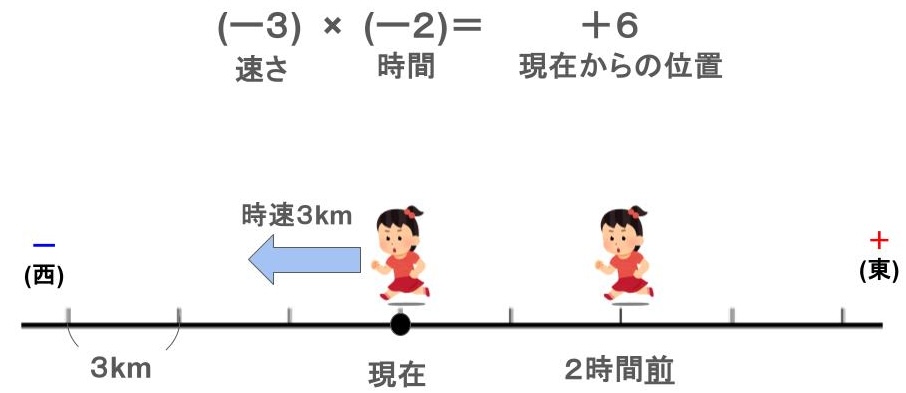
例 \((-3)\times(-2)\)の計算
\(+3\)と\(+2\)が共に負の数になっているので、求め方は
西の方向に時速3kmで歩いた時、2時間前の位置
答え 東に6km移動した場所
※時速は+を東の方向、ーを西の方向とし
時間は+を後の時間、ーを前の時間とします。

図にするとわかりやすいかも!

+とーはお互いに反対の意味があって
ー同士を組み合わせると+になるって考え方もあるね!

なんか漫画でありそうだね(笑)
乗法の仕組み(異符号)
(ー)✖️(+)=(ー)

もう例と図を確認すればいいね!
同じようにやっていきます。
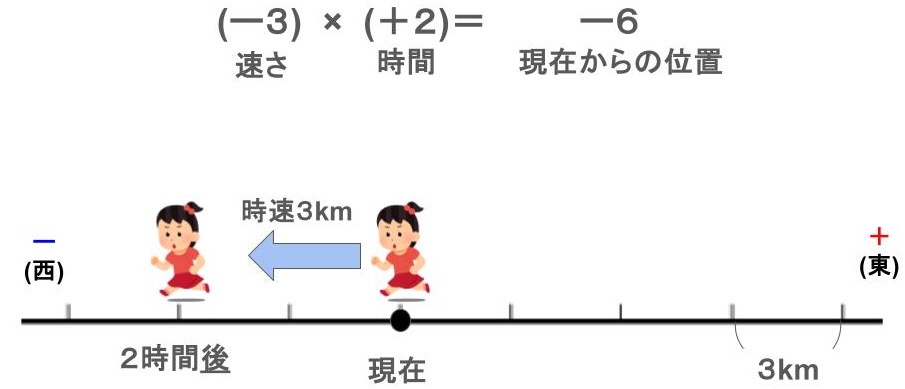
例 \((-3)\times(+2)\)の計算
求め方は
西の方向に時速3kmで歩いた時、2時間後の位置
答え 西に6km移動した場所
※時速は+を東の方向、ーを西の方向とし
時間は+を後の時間、ーを前の時間とします。
(+)✖️(ー)=(ー)
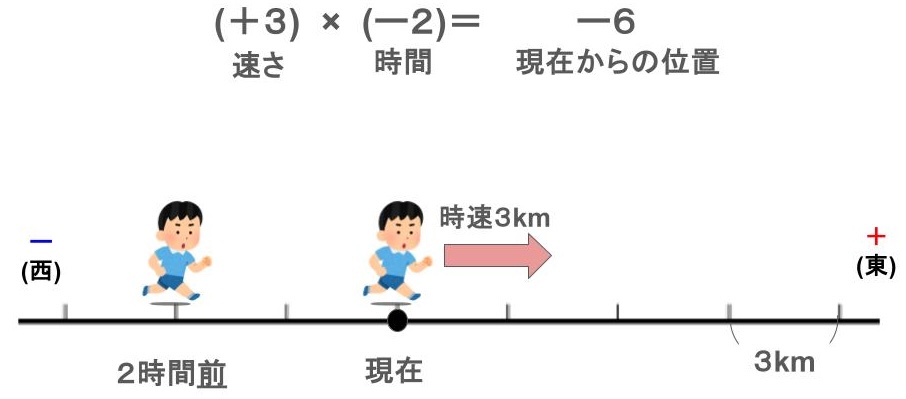
例 \((+3)\times(-2)\)の計算
求め方は
東の方向に時速3kmで歩いた時、2時間前の位置
答え 西に6km移動した場所
※時速は+を東の方向、ーを西の方向とし
時間は+を後の時間、ーを前の時間とします。

どちらかが(ー)だと、結果も(ー)になっちゃうんだね。

そうだね!
異符号の場合は、結果が(ー)になることは確認できたかな?
この考え方は正負の数は「基準」がもとになっていることから導き出されます。
正負の数については次を見てください。
練習問題
法則自体は難しくありません。
理解できたら、問題に取り組みましょう。
問 次の計算をしなさい
(1) \((+4)\times(+3)\)
(2) \((-7)\times(+9)\)
(3) \((-2)\times(-11)\)
(4) \((-\frac{2}{5})\times(+10)\)
(5) \((-\frac{9}{4})\times(-\frac{2}{3})\)
(6) \((-1)\times(-6)\)
(7) \(-(-6)\)
(8) \(0\times(-5)\)
ポイントは同符号か異符号かです!
(7)の問題はこの記事では初見ですが、隠れている数を考えてみて下さい。
練習問題 解答
解答
(1) \(12\)
(2) \(-63\)
(3) \(22\)
(4) \(-4\)
(5) \(\frac{3}{2}\)
(6) \(6\)
(7) \(6\)
(8) \(0\)
各計算を以下に書いておきます。
参考にして下さい!
(1)
\(\begin{align}
(+4)\times(+3) &= +(4\times3) \\
&= 12
\end{align}\)
(2)
\(\begin{align}
(-7)\times(+9) &= -(7\times9) \\
&= -63
\end{align}\)
(3)
\(\begin{align}
(-2)\times(-11) &= +(2\times11) \\
&= 22
\end{align}\)
(4)
\(\begin{align}
(-\frac{2}{5})\times(+10) &= -(\frac{2}{5}\times10) \\
&= -(\frac{2}{1}\times2) \\
&= -4
\end{align}\)
※約分忘れずに!
(5)
\(\begin{align}
(-\frac{9}{4})\times(-\frac{2}{3}) &= +(\frac{9}{4}\times\frac{2}{3}) \\
&= +(\frac{3}{2}\times\frac{1}{1}) \\
&= \frac{3}{2}
\end{align}\)
(6)
\(\begin{align}
(-1)\times(-6) &= +(1\times6) \\
&= 6
\end{align}\)
(7)
\(\begin{align}
-(-6) &= (-1)\times(-6) \\
&= +(1\times6) \\
&= 6
\end{align}\)
(6)と(7)からわかるように、\(-\)のところには\((-1)\)が隠れています。
そのことから次のことが言えます。
ある数と\(-1\)との積を求めることは、その数の符号を変えることと同じ
例
\(\begin{align}
-(+2) &= (-1)\times(+2) \\
&= -2
\end{align}\)
(8)
\(0\times(-5) = 0\)
\(0\)には何を掛けても\(0\)ですね。
まとめ(同符号か異符号かを意識しよう)

符号だけ意識すればあとは大丈夫だね!

絶対値の計算さえできれば大丈夫だね。
だけど、なぜ符号がそうなるかは理解しておこうね。
改めて乗法について確認です。
2つの正負の数の乗法
①同符号の数
➡︎絶対値の積に正の符号(+)をつける。
②異符号の数
➡︎絶対値の積に負の符号(ー)をつける。
ある数と\(-1\)との積を求めることは、その数の符号を変えることと同じ
例
\(\begin{align}
-(+2) &= (-1)\times(+2) \\
&= -2
\end{align}\)
今回は、ただの計算を図と小学校の計算を使って考えました。
そういった、計算のやり方を理解するために他方面の見方をして考えていくことは数学ならではの方法です。
手間はかかるかもしれませんが、知識を広げるために一つ一つ学んでいきましょう。
それでは!
コラム(速さについて)
速さについて以下の確認をしました。
速さ・時間・距離の関係
(距離)=(速さ)\(\times\)(時間)
(速さ)=(距離)\(\div\)(時間)
(時間)=(距離)\(\div\)(速さ)
これについては図の覚え方をした人が多いでしょう。
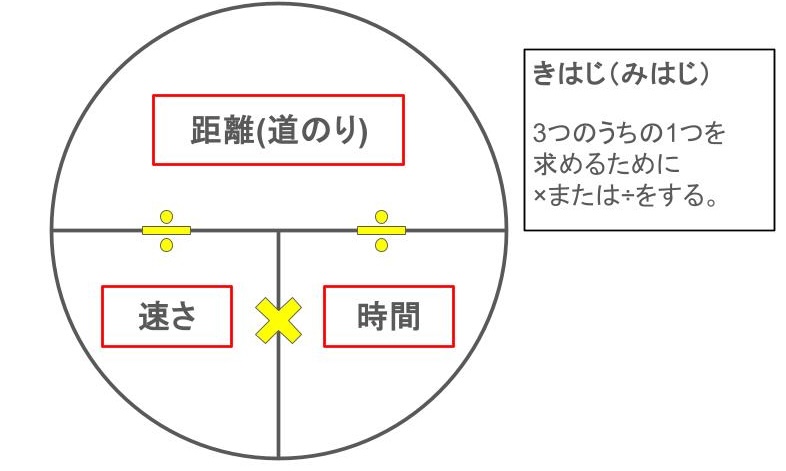
ここでは、「単位」を使った考え方をお伝えします。
単位について
速さ・時間・距離をそれぞれ、次の単位で置き換えます。
速さ・・・km/h(キロメートル毎時) ※1時間で進む距離
時間・・・h(時間)
距離・・・km(キロメートル)

なんで速さだけ「/」が入ってるの?

それは、速さの求め方を使えばわかるよ
(速さ)=(距離)\(\div\)(時間)
単位版
km/h = km \(\div\) h
割り算で求められますね。
単位にある「/」は(割る)の意味があります。
なので「/」は分数の真ん中の線(\(\frac{ }{ }\))と同じと思えばいいです。
普段、数字の割り算ですが、単位も一緒に割っています。
そのことを理解できれば、わかりやすいでしょう。
(距離)=(速さ)\(\times\)(時間)
単位版
km = km/h \(\times\) h
※km/hは\(\frac{km}{h}\)と同じなので、hで約分ができます。
(時間)=(距離)\(\div\)(速さ)
単位版
h = km \(\div\) km/h
h = km \(\times\) h/km (逆数をかける)
※km/hは\(\frac{km}{h}\)と同じです。
そして、割り算は逆数を掛ける事と同じです。そして約分をします。
(これに関しては別の記事で扱います。)
このように、単位で考えると求め方が割り算なのか、掛け算なのかを理解しやすくなります。
考え方の一つとして参考にして下さい。





コメント