こんにちは!ベーです。
今回は正負の数の除法について学んでいきます。

除法?何それ?

簡単に言えば「割り算」だね!

なるほどね!
(なんで分かりづらい言葉にするんだろ…)
今回は
・符号について
・計算方法について
扱っていきます。
割り算については小学校で扱っていると思いますが、
負の数が入った場合について考えていきます。
・負の数の除法を忘れてしまった
・逆数ってなんだったか忘れた
・そもそもなぜ逆数を掛けるのか
そんな人はぜひ最後まで見てください!
除法の計算
符号
次の計算ができるようになればOKです。
(1)\((+6)\div(-3)\)
(2)\((-6)\div(-3)\)

\(6\div3\)は\(2\)なんだけど、、
符号はどうなるんだろ?
絶対値(数字の部分)の計算は小学校でやってますよね。
符号がどうなるかですが、、
私が授業をしていた時ではこんな形で話をしました。

突然だけど、減法(引き算)を求めるために使ったのは
どんな計算?

そういえば、加法(足し算)だったね!

じゃあ、除法を求めるために使うのは?

残ってる乗法か!
このように
加法↔︎減法と乗法↔︎除法
と2つの計算に関連があるように話をしていきました。
それでは、先ほどの例を使って考えましょう。
例 次の計算をしなさい。
(1)\((+6)\div(-3)=\)◻︎
(2)\((-6)\div(-3)=\)◻︎
それぞれ求める答えを◻︎としてこの計算を乗法に変えてみましょう。

割り算を掛け算に直すから。。
例を乗法に直すと
(1)◻︎\(\times(-3)=+6\)
(2)◻︎\(\times(-3)=-6\)
よくわからない人は符号を外したバージョンで考えてみて下さい。
小学校の復習になります!
除法を乗法に置き換える
\(6\div3=\)⚪︎(6を3等分すると⚪︎ずつに分けられる)
➡︎⚪︎\(\times3=6\)(⚪︎が3セットあれば合計6になる)

それでは符号を考えてみよう!
◻︎に入る符号はどうなるかな?

同符号は(+)で異符号は(ー)だから。。
(1)は(ー)で(2)は(+)!
そうなると、例の解答は
例(解答) 次の計算をしなさい。
(1)\((+6)\div(-3)=-2\)
(2)\((-6)\div(-3)=+2\)

これって乗法の符号と同じだよね。
そうです!次のことがいえますね。
2つの正負の数の除法
①同符号の数
➡︎絶対値の商に正の符号(+)をつける。
②異符号の数
➡︎絶対値の商に負の符号(ー)をつける。
※商は割り算の結果を意味します。
見覚えがあるかもしれませんが、乗法と全く同じです。
乗法については以下を見て下さい。
数字の計算
符号について理解できれば、あとは数字の計算です。

計算ってどうやるんだっけ?

割り算は、逆数をかければいいよ!
なぜ、逆数をかければいいのかは最後に載せていますので、
気になる人は見てください。
復習(割り算の計算)
割り算の計算は逆数を掛ければ良い
\(\begin{align}
\frac{6}{5}\div\frac{3}{10} &= \frac{6}{5}\times\frac{10}{3} \\
&= \frac{2}{1}\times\frac{2}{1} \\
&= 4
\end{align}\)
負の数の逆数

そうやるのか!
でも、負の数の逆数ってなんだろ?
それは、逆数の意味を考えれば簡単です。

逆数の意味って…?
逆数
2つの数の積が1の時、もう一方の数を他方の数の逆数という。

この意味から、掛けて1になるような数が逆数になることがわかるね。
そしたら、\(\begin{align}-\frac{1}{2}\end{align}\)の逆数は、、?

掛けて1になるから、、、
\(-2\)だ!

正解!
だから、負の数の逆数も負の数になるね!
逆数
2つの数の積が1の時、もう一方の数を他方の数の逆数という。
一方の数が正の数の時、逆数も正の数
一方の数が負の数の時、逆数も負の数になる
例題
それでは、実際の例題に入っていきます。
例題 次の計算しなさい
(1)\(\begin{align}\frac{9}{8}\div(-\frac{3}{4})\end{align}\)
(2)\(\begin{align}9\div(-\frac{15}{4})\times(-5)\end{align}\)

基本は、逆数を掛ければいいんだね!

そう!
結局は掛け算になるので、3つ以上の計算でも乗法だけの時と同じようにやるよ。
前回の内容は以下を見てください。
例題 解答
(1) 逆数を求めることができれば、あとは約分をするだけです!
\(\begin{align}
\frac{9}{8}\div(-\frac{3}{4}) &= \frac{9}{8}\times(-\frac{4}{3}) \\
&= -(\frac{9}{8}\times\frac{4}{3}) \\
&= -(\frac{3}{2}\times\frac{1}{1}) \\
&= -\frac{3}{2}
\end{align}\)
(2)
\(\begin{align}
9\div(-\frac{15}{4})\times(-5) &= 9\times(-\frac{4}{15})\times(-5) ・・①\\
&= +(9\times\frac{4}{15}\times5) \\
&= +(3\times\frac{4}{1}\times1) \\
&= 12
\end{align}\)
①:逆数にするのは\(\div\)の直後の数字のみです。
その後ろの\(-5\)はそのままにしてください。

\(\div\)の直後を逆数に!だね!
練習問題
問 次の計算をしなさい
(1) \(\begin{align}(-\frac{2}{3})\div(-\frac{3}{7})\end{align}\)
(2) \(\begin{align}(-\frac{8}{3})\div2\end{align}\)
(3) \(\begin{align}\frac{2}{5}\div(-2^2)\times3\end{align}\)
(4) \(\begin{align}(-4)\div(-3)^2\div\frac{2}{5}\end{align}\)
(5) \(\begin{align}9\div\{(-\frac{15}{4})\times(-5)\}\end{align}\)
ここで累乗が登場しています。
逆数にする前にまず累乗から計算しましょう。
(5) 例題に加えて\(\{\}\)が加わっています。
これが入るだけで計算は大きく変わるので注意してみてください。
初めて見る人は\(\{\}\)の意味と優先順位から考えてみてください。
練習問題 解答
(1) \(\begin{align}\frac{14}{9}\end{align}\) (2) \(\begin{align}-\frac{4}{3}\end{align}\)
(3) \(\begin{align}-\frac{3}{10}\end{align}\) (4) \(90\)
(5) \(\begin{align}\frac{12}{25}\end{align}\)
各計算を以下に書いておきます。
(5)は例題と異なる答えですが、
\(\{\}\)が入っただけで変わってしまうことを知っておきましょう。
乗法の符号を決める計算は所々で省略しています。
(1)
\(\begin{align}
(-\frac{2}{3})\div(-\frac{3}{7}) &= (-\frac{2}{3})\times(-\frac{3}{7}) \\
&= (-\frac{2}{3})\times(-\frac{7}{3}) \\
&= \frac{14}{9}
\end{align}\)
(2)
\(\begin{align}
(-\frac{8}{3})\div2 &= (-\frac{8}{3})\times\frac{1}{2} \\
&= -\frac{4}{3}
\end{align}\)
(3)
\(\begin{align}
\frac{2}{5}\div(-2^2)\times3 &= \frac{2}{5}\div(-4)\times3 ・・①\\
&= \frac{2}{5}\times(-\frac{1}{4})\times3 \\
&= -\frac{3}{10}
\end{align}\)
①:まずは累乗から計算しましょう。
(4)
\(\begin{align}
(-4)\div(-3)^2\div\frac{2}{5} &= (-4)\div9\div\frac{2}{5} \\
&= (-4)\times\frac{1}{9}\times\frac{5}{2} \\
&= -\frac{10}{9}
\end{align}\)
(5)
\(\begin{align}
9\div\{(-\frac{15}{4})\times(-5)\} &= 9\div\frac{75}{4} ・・①\\
&= 9\times\frac{4}{75} \\
&= 3\times\frac{4}{25} \\
&= \frac{12}{25}
\end{align}\)
①:計算は基本左からですが、\(\{\}\)がある場合はこの中が優先になります。
今回は、逆数にする前に\(\begin{align}(-\frac{15}{4})\times(-5)\end{align}\)から計算をしましょう。
まとめ(逆数と計算の順序に注意!)
いかがでしたか?
除法の計算方法は
・符号は負の数の数で決まる。
・割り算は逆数を掛ける。
この2つで求めることができます。

じゃあ掛け算ができればいいね!
基本はそうですね。
あとは、計算の順序に気をつけてください。
それでは!
コラム(逆数を掛ける理由)
今回、除法は逆数を掛けることをお伝えしましたが
その理由について解説します。
理由1(分数の分母を1にして整理する)
この理由だけ聞いても訳わからないと思うので計算をやってみます。
例
\(\begin{align}
2\div\frac{5}{6}
\end{align}\)

教員時代、「逆数を掛けるよ」って教えていたんだけど
実際にこういう計算をする子がいたんだ。
解答例
\(\begin{align}
2\div\frac{5}{6}=\frac{2}{\frac{5}{6}}
\end{align}\)

割り算って割る数を分母に持っていけばいいんだよね!
でもこれってこの後どうすればいいの?
なんか分数に分数があって気持ち悪い。。

それは、整数同士の計算で習ったことだよね。
\(\begin{align}
2\div3=\frac{2}{3}
\end{align}\)みたいに
実際に習ってきたことを活用していますが、これは逆数を掛けるに繋がる計算なんです!
その解決策としては

分数に分数って気持ち悪いよね。
そしたら、分母の分数を1にしてみよっか!

分母を1に?それって約分ってこと?

そうそう!
分母が分数でも約分することはできるよ!
実際の計算をしてみましょう。
分母にある\(\begin{align}\frac{5}{6}\end{align}\)が1になるようにするには
逆数である\(\begin{align}\frac{6}{5}\end{align}\)をかける必要がありますね。
そして、約分なので分母と分子の両方に\(\begin{align}\frac{6}{5}\end{align}\)を掛けましょう!
解答例(続き)
\(\begin{align}
2\div\frac{5}{6}&=\frac{2}{\frac{5}{6}} \\
&=\frac{2\times\frac{6}{5}}{\frac{5}{6}\times\frac{6}{5}} \\
&=\frac{2\times\frac{6}{5}}{1} \\
&=2\times\frac{6}{5} ・・① \\
&=\frac{12}{5}
\end{align}\)

①のタイミングで逆数を掛けている式と同じになるよね!

ほんとだ!じゃあ分母を分数にしたことはただ遠回りをしていたことに過ぎないんだね!
割る数を分母に持って行く方法から逆数を掛ければいいことが導けましたね。
理由2(通分してから考えてみる)
例
\(\begin{align}
\frac{1}{2}\div\frac{3}{8}
\end{align}\)
授業していると他にもこんな計算をする生徒がいました。
解答例
\(\begin{align}
\frac{1}{2}\div\frac{3}{8}&=\frac{4}{8}\div\frac{3}{8}
\end{align}\)

分数の計算って通分するんだよね!

それは加法と減法のときだけの計算で、、
(いやちょっと待てよ)
ここでこんな図を用意してその後の計算を考えてみました。
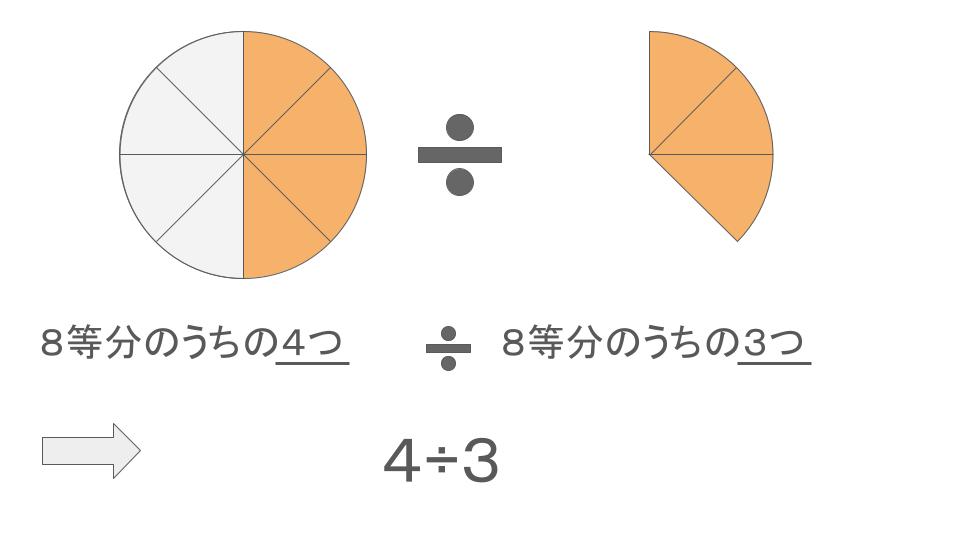

\(\begin{align}\frac{4}{8}\div\frac{3}{8}\end{align}\)のように分母を揃えれば、
結局は分子の数だけ考えればいい計算できるね!
もしよくわからない人は
整数同士の計算も分母が1同士で計算していると考えればいいよ
例
\(2\div3\)は\(\begin{align}\frac{2}{1}\div\frac{3}{1}\end{align}\)をやってることと変わらない

なるほど!じゃあ答えは\(\frac{4}{3}\)か!

だね!じゃあこの計算を書き出してみよう。
図で示すと簡単ですが、これを式に表すと少し複雑です。
解答例(図の考え方が逆数を掛けることと同じであることの説明)
\(\begin{align}
\frac{1}{2}\div\frac{3}{8}&=\frac{4}{8}\div\frac{3}{8} \\
&= 4\div3 ・・①\\
&= \frac{4}{3} ・・②\\
&= \frac{8}{6} ・・③\\
&= \frac{1\times8}{2\times3} \\
&= \frac{1}{2}\times\frac{8}{3} \\
\end{align}\)

①では図で示した計算をしているよ。
本来は②で終わりなんだけど、逆数を掛けることを説明しているから
最終的に\(\begin{align} \frac{1}{2}\times\frac{8}{3} \end{align}\)になることを表しているよ。
③から訳わからなくなりそうになりますが、目標は逆数をかけていることを示すための計算をしています。

整数の割り算は分母1でやっていた事と変わらないんだね!
それで通分に意味あることが納得できたよ。
これら2つに関しては、理由の説明なので理解できたら「逆数を掛ける」で素早く計算してくださいね!





コメント