こんにちは!ベーです。
皆さんは、数学を学ぶときよく考えることがありませんか??
それは
「数学って何のためにやるの?」
「三平方の定理って将来役立たなくね??」
です。ベーも教師をしていて、たくさんの生徒に質問されてきました。。笑
ちなみに、数学を学ぶ意味は、学習指導要領として文部科学省が以下のように定められていますが、
数学的な見方・考え方を働かせ,数学的活動を通して,数学的に考える資質・能力を次のとおり育成することを目指す。
(1) 数量や図形などについての基礎的な概念や原理・法則などを理解するとともに,事象を数学化したり,数学的に解釈したり,数学的に表現・処理したりする技能を身に付けるようにする。
(2) 数学を活用して事象を論理的に考察する力,数量や図形などの性質を見いだし統合的・発展的に考察する力,数学的な表現を用いて事象を簡潔・明瞭・的確に表現する力を養う。
(3) 数学的活動の楽しさや数学のよさを実感して粘り強く考え,数学を生活や学習に生かそうとする態度,問題解決の過程を振り返って評価・改善しようとする態度を養う。
中学校学習指導要領 (平成 29 年告示) 解説 数学編 文部科学省
・・・
いやどういうこと???
ですよね( ´•̥̥̥ω•̥̥̥` )
なので、元数学教師のベーが指導をしてく中で感じた理由をお伝えしたいと思います!
それでは見ていきましょう!
理由1:問題が解けた時が気持ちいい!
ゲームや計算が好きな人は算数をやっていて、こう感じたことはないでしょうか?

「・・・やっとクリアできたー!」
「気持ちいいー!」
んでこの後、、、

「次のステージは??」
「もっとむずいの来い!」
ってなりますよね??
だってできるものは楽しいですもん。
こういった達成感の対象を数学に持っていくことができれば、、、
数学をゲームやパズルのように扱ってどんどん学べる!
数学は1問につき1答であり、今まで学んだこと(武器)を組み合わせて解いていきます。
そのため、問題をゲーム上の敵のように扱うことができれば、勝ったものでしょう。
例えば
例えば、数学が好きな生徒はこのように問題を解く時、、
問題
〇〇の時、△△だった。この時、◻︎◻︎の場合の時の××の値を求めなさい。
こんな形で考えて解いていましした。
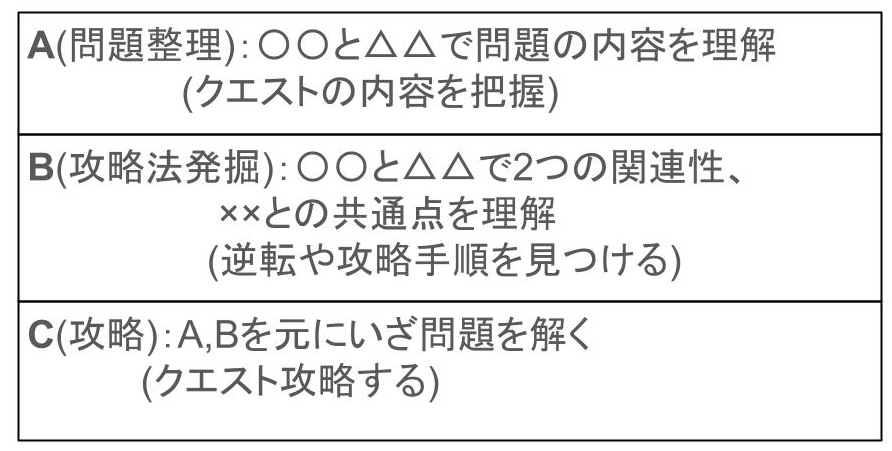

A,B,C の順番で考えてたよ。
Aには言葉の意味や求められていることを理解すること
Bには覚えた公式や法則を活用できること
Cには計算過程でも目的を見失わずに、自分の力で解き進める実行力があること
それぞれこれらの力が必要になると思うよ!
ただ、、
これを見てわかるかもしれませんが、
この理由で納得できるのは
・数学がある程度できる人
であって

数学なんて知らねーよ
ふざけんな、数学なくなんねーかな
という人には厳しいかもしれません。。
ただ、継続して努力して数学の知識が身についていけば
問題が解けた時の気持ちよさで
数学を学ぶ意味に繋がるのではないかと思います。
理由2:問題解決能力が身につく【論理的思考】
問題解決能力として論理的思考が求められます。
論理的思考??何それ?
と思っている人に説明すると
論理的思考力
論理に基づいて思考する能力(の高さ)という意味で用いられる表現。道理や筋道に則って思考を巡らせて結論を導いたり、あるいは、複雑な事柄を分かりやすく説明したりできる能力として主に捉えられる。
weblio辞書 (論理的思考力)
要は、与えられた事柄を整理して、わかりやすく伝える能力です。
論理的思考力がないと
例えば、クラスで行事を成功させるために取り組むことを考える時

・あれがいいよ
・いやいやこれがいい!
・俺なんでもいいや
のように話がまとまらない、または

なんとなくでこれでいいんじゃない?

(意見出なそうだし、、)
いいじゃんそうしよう。
それかその場でふと出た意見に流されませんか?
学級担任をやっていた経験としては、

意見出すぎてまとまらねーなー、、
この子たちはゴールを見据えているのかな??
と感じたことが多々ありました。。。
もしかしたら私の実力不足かもしれませんが、、(泣)
論理的思考力があると
ただ、論理的思考力があれば
ゴールに向かってよりよく考えることができるようになるんです。
例えば、先ほどのクラスの問題に対して、

・うちのクラスの目的は〇〇
(道筋を立てるための目的の確認)
・〇〇や△△の意見が出ているから(道筋に沿って思考を巡らせる)
・目的に近づけるには〇〇したらいいんじゃないか!
(わかりやすい結論の決定)
目的に対して、何が必要か、どう辿ればいいのかを考えながら進めて
理想の結論へと到達しやすくなるのです!
このことと数学がどう繋がるのかですが、、
数学は、
定義や定理などの公式や図形の性質を活用して、問題を解決する
これの繰り返しです。
具体的に言えば、
・問題解決(目的の確認)
・解答のために持っている知識を使って考える(道筋に沿って思考を巡らせる)
・解答、記述(結論の決定、わかりやすい説明)
ということになります。
そして、それがある程度決まっているので分かりやすいんです!
この流れを理解し、スムーズに取り組むことができれば、
この対象が数学以外のことになっても数学での取り組みが活かせるはずです。
理由3:理科の基礎基本になる
算数の勉強をしているとあまり実感ないかと思いますが、中学に入ると数学の使われ方が実感できるかと思います。
主に、理科ですね。
例えば、
・像や虚像の問題には「図形の移動」
(対称移動)の考え方
・運動の記録には「グラフをまとめる必要」がある
・収集データの「代表値(平均値など)の活用」
・化学反応式の基本は、数学の「方程式」
などなど、理数系とも言われるほど、科学分野とのシナジーは凄まじく
実際に「数学でやったと思うけど」と言われてしまうぐらいです。
私が教員をしていた時に、理科の担当の先生と話していて

ベー先生ここの単元で連立方程式扱うんだけど
もう数学でやってるよね?
のように聞かれて理科の授業を行なっていなくても繋がりを感じることが多くありました。
高校に入るとより抽象的になり、『何のためにやっているのか、、』
と迷子になりかけますが、理科が好きな人は数学は大事な土台なので苦せずに学び続けましょう!
まとめ:数学を学ぶ意味は人それぞれ
いかがでしたでしょうか。
数学あるあるの
「数学って何のためにやるの?」
「三平方の定理って将来役立たなくね??」
に3つの理由から考えてみました。
ベー自身は「理由2:論理的思考力が身につく」が数学を学ぶ理由としてはベストだと思います。
将来的に役に立つ力でもあるので!
ただ、見出しにもある通り、学ぶ理由づけは人それぞれ。
何を理由にするにしても数学を楽しむきっかけにつながってくれたら嬉しいです。
それでは!


コメント