こんにちは!ベーです。
今回は、乗法の計算方法について少し深掘りします。

乗法のやり方は前回習ったよね?

基本の部分は習ったね!
今回は、次のような計算式を扱うよ。
(1) \((-8)\times3\times(-5)\)
(2) \((-4)^2\times(-4^2)\)
今回はこのような計算式が解けることが目標になります。
・乗法の結合法則、交換法則を学びたい人
・積の符号をすぐ答えられるようになりたい人
・累乗について確認したい人
・乗法の計算が早くなりたい人
はぜひチェックしてください!
計算の工夫や、累乗について学んで計算力を上げていきましょう!
乗法の基本はこれを確認して下さい。
いくつかの数の積
まずは、3つ以上の数の掛け算からやります。
例題をもとに計算しましょう。
例 次の計算をしなさい。
\((-8)\times3\times(-5)\)

えーと左から計算するから
まず異符号でそのあとは、、

ちょっと待って!
加法の時みたいに工夫してやろ!
計算の基本は左からですが、2つの法則を使って工夫をしましょう!

2つの法則ってまさか、、
乗法の交換法則、結合法則
乗法にも加法と同じく、結合法則と交換法則があります。
乗法の交換法則
\(a \times b = b \times a \)
※数字を交換して掛け算できる!
乗法の結合法則
\( (a \times b) \times c = a \times (b \times c) \)
※数学では()の中身から先に計算します。
なので、左の2つから計算することと、右の2つから計算することは同じですよ〜という法則です。
これらの法則を使って例を解いていきます。
今回は2つを無理やり使うので、遠回りな解き方になります。
実際の計算については練習問題の解答を参考にして下さい!
例 解答
\(\begin{align}
(-8)\times3\times(-5) &= 3\times(-8)\times(-5) ・・・(1) \\
&= 3\times{(-8)\times(-5)} ・・・(2)\\
&= 3\times40\\
&= 120
\end{align}\)
(1)交換法則で\(-8\)と\(3\)を入れ替える。
(2)結合法則で\((-8)\times(-5)\)から計算する。

この法則ってなんの目的でやるの?

各自がやりやすい計算をするためだね!
ベーの場合は、
・同符号の計算をしたい
・0がつく数字を作りたい(今回は40とか)
を目的にしているよ!
法則はあくまで手段で、自分がどういう計算をすると早くできるかに焦点を当てて取り組んでみましょう!
符号を先に決める

でも、毎回法則を意識するのもめんどくさいよ

そしたら、符号を先に決定する方法でやってみよう!
先ほどとは違う式を例題にして扱っていきます。
例 次の計算をしなさい。
\((-\frac{1}{2})\times6\times(-1)\times(-2)\)

この計算の答えの符号は何になると思う?

(ー)が2つの時は、同符号で(+)になるから、3つの時は(ー)かな!
・・・☆

その通り!その調子で考えると法則性があるよね?

(ー)が2, 4, 6・・って偶数の時は(+)で
(ー)が1, 3, 5・・って奇数の時は(ー)だ!
すーやは考えの過程が省略されていますが、☆のところの考え方を活用すれば次のことがいえます。
積の符号
- 負の数が偶数個あれば(+)
例 (ー)×(ー)→(+)、(ー)×(ー)×(ー)×(ー)→(+) - 負の数が奇数個あれば(ー)
例 (ー)×(ー)×(ー)→(+)
この考えを活用すると
例 解答
\(\begin{align}
(-\frac{1}{2})\times6\times(-1)\times(-2) &= -(\frac{1}{2}\times6\times1\times2) ・・・(1) \\
&= -(\frac{1}{2}\times2\times1\times6) ・・・(2)\\
&= -(1\times6)\\
&= -6
\end{align}\)
(1)負の数が奇数個あるので、答えの符号は(ー)
(2)交換法則で、約分をやりやすいようにする。

最初から符号を決めちゃえばあとは小学校の計算と変わらないね!
そうなんです!
この方法は、小学校の計算に落とし込むことができる方法なんです、

どちらも適切な方法なので、自分のやりやすい計算を選択してね。
累乗
続いて次の問題に取り組みましょう。
例 次の計算をしなさい。
\((-4)^2\times(-4^2)\)

累乗は上の数字分だけ掛け算すればいいんだよね!
累乗
指数(上の数字)の分だけ掛け算をする
例
\(5^2=5\times5\)

そうだね!今回は例題のように、負の数の累乗を解けるようにしよう。
例題はこの2つの違いが分かればいいです。
\((-4)^2\) と \(-4^2\) の違い

似てるけど何が違うんだろ?

ポイントは指数の位置だよ
負の数の累乗
・指数が数字の隣にあるのか、()の隣にあるかで意味が変わる。
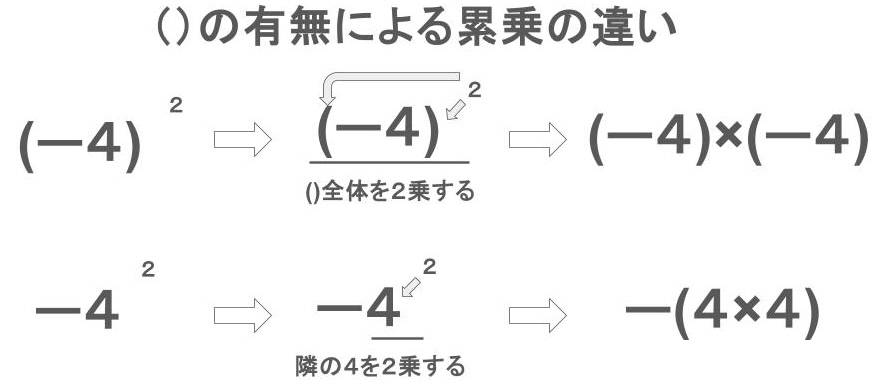
上の画像から例題を解くとこうなります。
例 解答
\(\begin{align}
(-4)^2\times(-4^2) &= (-4)\times(-4)\times(-4\times4) \\
&= 16\times(-16) \\
&= -256
\end{align}\)

ポイントは指数の位置だね!
練習問題
問 次の計算をしなさい
(1) \((-2)\times5\times(-7)\times6\)
(2) \((-\frac{7}{3})\times6\times(-5)\times(-2)\)
(3) \(\frac{5}{3}\times(-\frac{9}{10})\times4\)
(4) \((-1)^5\)
(5) \((-\frac{2}{3})^2\)
(6) \(-3^2\times(-2^3)\)
計算のルールに従って丁寧に解いて下さいね。
解答
(1) \(420\)
(2) \(-140\)
(3) \(-6\)
(4) \(-1\)
(5) \(\frac{4}{9}\)
(6) \(72\)
各計算を以下に書いておきます。
(1)〜(3)は法則や符号を先に決める方法があります。
計算ではどちらかしか書きませんが、皆さんはやりやすい方でやってみて下さい。
(1)
\(\begin{align}
(-2)\times5\times(-7)\times6 &= +(2\times5\times7\times6) \\
&= 420
\end{align}\)
(2)
\(\begin{align}
(-\frac{7}{3})\times6\times(-5)\times(-2) &= -14\times10 \\
&= -140
\end{align}\)
※結合法則を活用しています。
(3)
\(\begin{align}
\frac{5}{3}\times(-\frac{9}{10})\times4 &= -(\frac{5}{3}\times\frac{9}{10}\times4) \\
&= -(\frac{1}{1}\times\frac{3}{1}\times2) ・・・(1)\\
&= -6
\end{align}\)
※(1)は約分を表現しています。実際の記述では書く必要はありません。
(4)
\(\begin{align}
(-1)^5 &= (-1)\times(-1)\times(-1)\times(-1)\times(-1) \\
&= -1
\end{align}\)
(5)
\(\begin{align}
(-\frac{2}{3})^2 &= (-\frac{2}{3})\times(-\frac{2}{3}) \\
&= \frac{4}{9}
\end{align}\)
(6)
\(\begin{align}
-3^2\times(-2^3) &= -(3\times3)\times\{-(2\times2\times2)\} \\
&= -9\times(-8) \\
&= 72
\end{align}\)
※記号を続けて書くことはできないので(今回は\(-\times\))
かっこ()を使いますが、()は\((2\times2\times2)\)で使用しているので
中かっこ{}を使っています。
まとめ(符号と指数に注意!)
いかがでしたか?
・符号は負の数の個数
・累乗は指数の位置
に気をつけて計算をしていきましょう。
改めて、法則と乗法について確認です。
乗法の交換法則
\(a \times b = b \times a \)
※数字を交換して掛け算できる!
乗法の結合法則
\( (a \times b) \times c = a \times (b \times c) \)
※数学では()の中身から先に計算します。
なので、左の2つから計算することと、右の2つから計算することは同じですよ〜という法則です。
積の符号
- 負の数が偶数個あれば(+)
例 (ー)×(ー)→(+)、(ー)×(ー)×(ー)×(ー)→(+) - 負の数が奇数個あれば(ー)
例 (ー)×(ー)×(ー)→(+)
累乗
指数(上の数字)の分だけ掛け算をする
例
\(5^2=5\times5\)
負の数の累乗
・指数が数字の隣にあるのか、()の隣にあるかで意味が変わる。
次は除法(割り算)に入りますが乗法の要素も入ります。
演習を繰り返して、やり方を身につけていきましょう!
それでは!




コメント