こんにちは！べーです。
今回は正負の数の加法について学んでいきます！
加法って言葉を使ってますが、ただのたし算ですね（笑）
でもたし算なのに「ー」が入ったりわけ訳わかんないよ
「ー」や（）があって見づらいと思うけど、数直線から考えれば大丈夫！
そうです。正負の数は数直線が基本です。
慣れたら、ルールがあるのでそれを覚えてしまいましょう！
今回は例題をいくつか扱っていきます！
加法（例題）
早速、例題を扱いましょう。
例題
次の計算をしなさい。
(1) \((+3)+(+5)\)
(2) \((-2)+(-4)\)
(3) \((-1)+(+4)\)
(4) \((+6)+(-7)\)
加法の基本はこの例題の４種類です！
言葉に直すと次の通りです！
(1) 正の数同士
(2) 負の数同士
※(1),(2)は同符号と言われます。
(3) 正の数と負の数で
絶対値が正の数が大きい
(4) 正の数と負の数で
絶対値が負の数が大きい
※(3),(4)は異符号と言われます。
同符号、異符号って授業で言ってた気がするなー
絶対値って確か。。。
絶対値？？の人は次の投稿を確認して復習しましょう！
今回、＋の両隣に（）がありますが正負の数は号（＋,ー）と数字がセットになっているためです。
今後、（）が外れますがそれは別の回で触れます。
では、解答・解説です。
加法（例題の解答）
解答
(1) \(+8\)
(2) \(-6\)
(3) \(+3\)
(4) \(-1\)
全ての問題で数直線で考えましょう。
数直線では、符号（＋,ー）が左右、絶対値が移動を表します。
同符号の加法
(1) 図に表すとこのようになります。
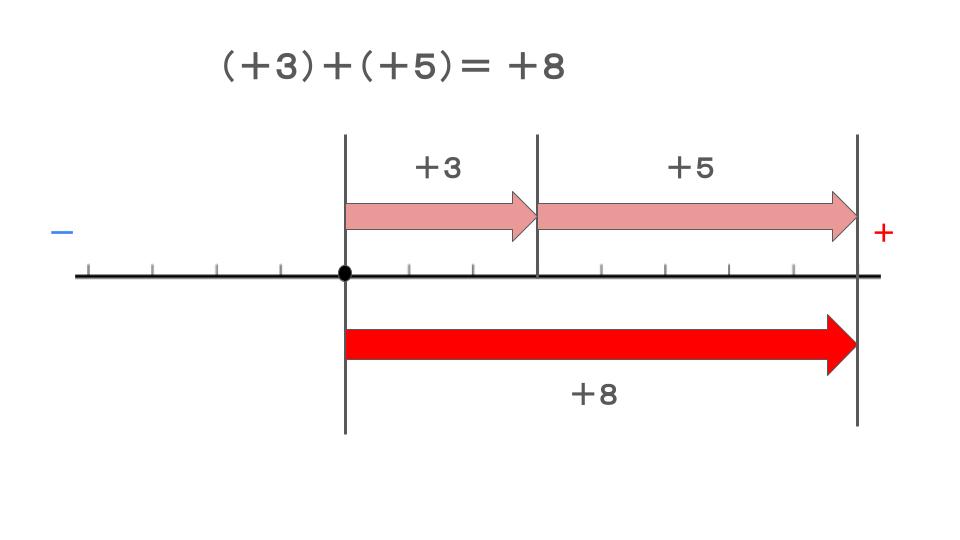
同じ符号なので、方向も同じです。
なので、符号は同じで絶対値を足したものが解答になります。
\(+(3+5)=+8\)
(2) 図に表すとこのようになります。
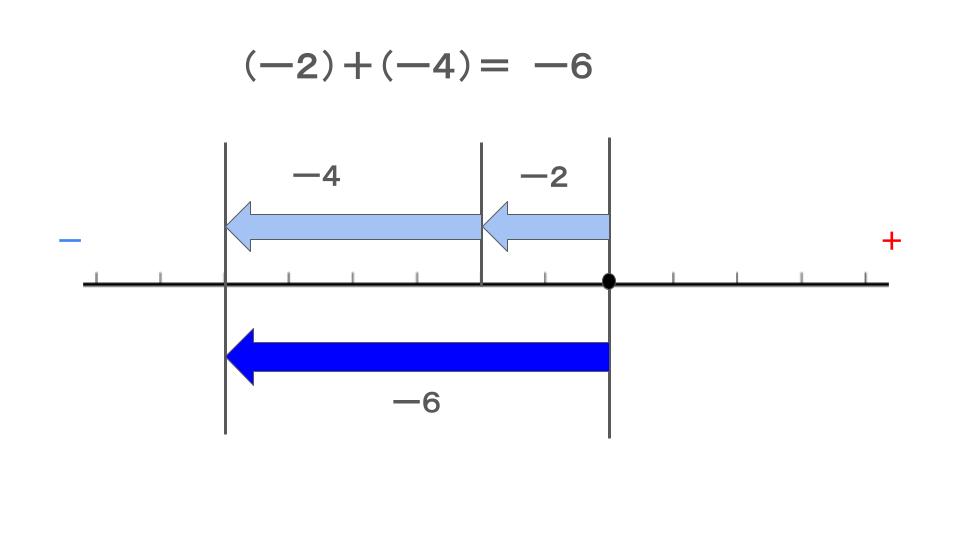
(1) と同じパターンですね。
方向が負の方向（左側）になるだけです。
解答は、同じ符号で絶対値を足したものです。
\(-(2+4)=-6\)
ここで同符号の時をまとめておきましょう。
同符号の加法
同じ符号をつけて、絶対値を足す！
同符号は同じ符号！
異符号の加法
(3) 図に表すとこのようになります。
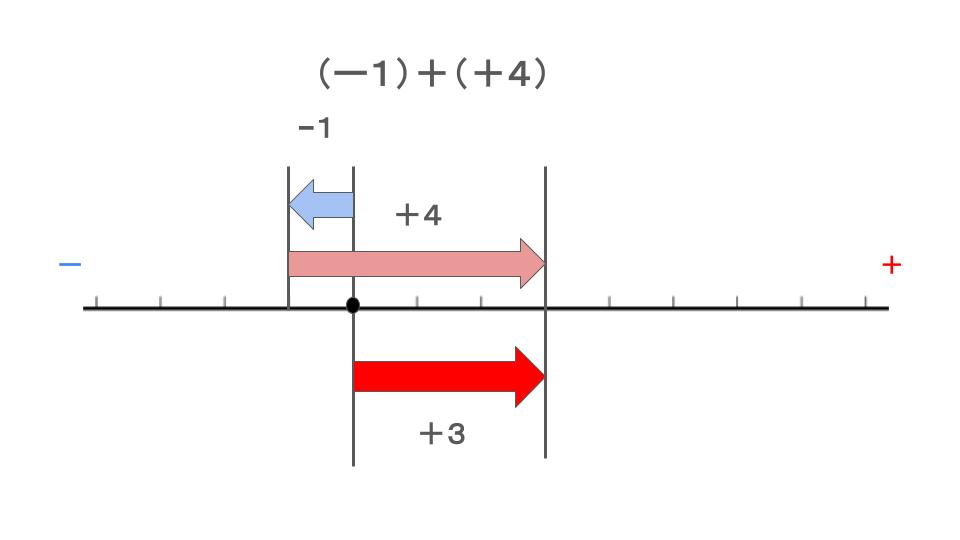
順に進めていくと、
左に１移動して、右に４移動する。
その結果は基準（⚫︎）から右に３ある。
よって、＋３が解答になります。
※あくまで、解答は基準からどっちにいくつ離れているかで判断してください！
ここで図をよく見てください。
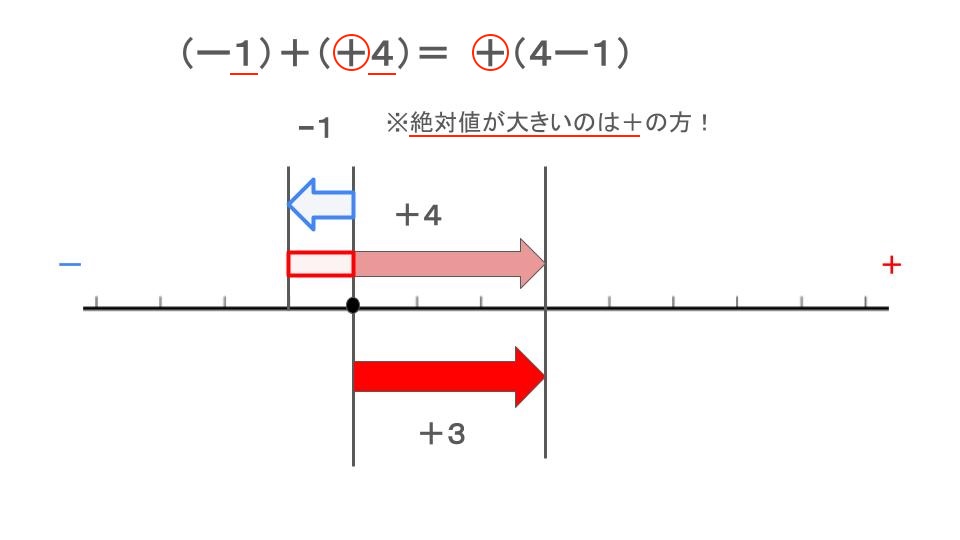
薄い部分って、往復分無駄に移動していません？
これって、被っているところは消して考えれば良くない？
そう！
消すってことは引き算だね！
ここで、加法に引き算要素が入ります。
\(+(4-1)=+3\)
(4) 図にするとこの通り
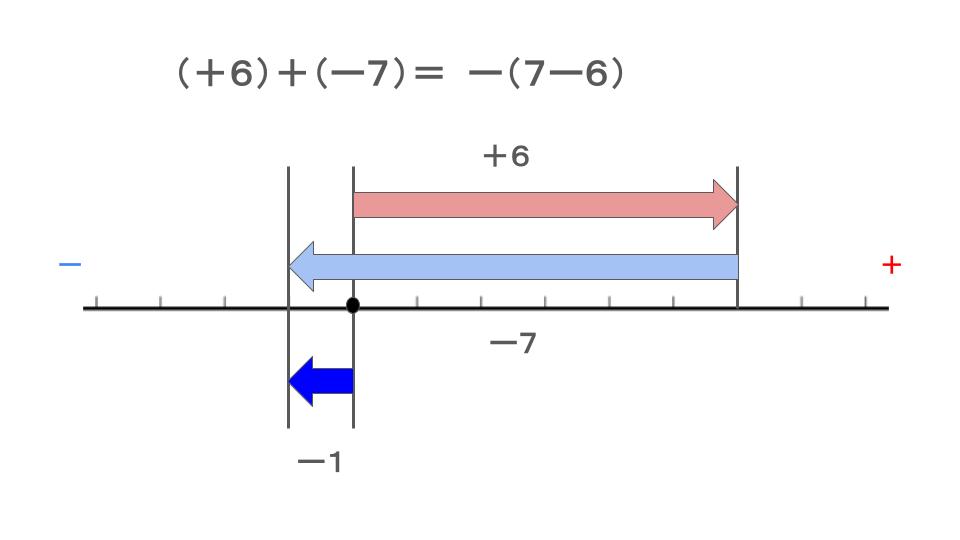
負の数の絶対値が大きいので、最終地点は左側（負の方向）になります。
被っている部分を消して考えてみましょう。
引く時は大きい方から小さい方です！
\(-(7-6)=-1\)
異符号の加法についてまとめましょう。
異符号の加法
符号・・ 絶対値の大きい方
数字・・（大きい数字）ー（小さい数字）
足し算が同符号か異符号かで見分ければいいね！
最初は覚えるのが大変かもしれませんが、無意識でできるくらいやってみてください。
練習問題
問 次の計算をしなさい。
(1) \((+1)+(+8)\)
(2) \((-7)+(-2)\)
(3) \((-4)+(+10)\)
(4) \((+3)+(-8)\)
(5) \((+3)+(-3)\)
(6) \((-0.3)+(-2.2)\)
(7) \((-\frac{1}{6})+(+\frac{1}{4})\)
(8) \((+\frac{1}{10})+(-\frac{3}{5})\)
まとめに書いたことを1つずつ丁寧にやっていきましょう！
練習問題 解答
解答
(1) \(+9\)
(2) \(-9\)
(3) \(+6\)
(4) \(-5\)
(5) \(0\)
(6) \(-2.5\)
(7) \(+\frac{1}{12}\)
(8) \(-\frac{2}{5}\)
各計算を以下に書いておきます。
参考にしてください！
(1)
\(\begin{align}
(+1)+(+8) &= +(1+8) \\
&= +9
\end{align}\)
(2)
\(\begin{align}
(-7)+(-2) &= -(7+2) \\
&= -9
\end{align}\)
(3)
\(\begin{align}
(-4)+(+10) &= +(10-4) \\
&= +6
\end{align}\)
(4)
\(\begin{align}
(+3)+(-8) &= -(8-3) \\
&= -5
\end{align}\)
(5)
\((+3)+(-3) = 0\)
※\(0\)には符号は付きません！
(6)
\(\begin{align}
(-0.3)+(-2.2) &= -(2.2+0.3) \\
&= -2.5
\end{align}\)
(7)
\(\begin{align}
(-\frac{1}{6})+(+\frac{1}{4}) &= +(\frac{1}{4}-\frac{1}{6}) \\
&= +(\frac{3}{12}-\frac{2}{12}) \\
&= +\frac{1}{12}
\end{align}\)
(8)
\(\begin{align}
(+\frac{1}{10})+(-\frac{3}{5}) &= -(\frac{3}{5}-\frac{1}{10}) \\
&= -(+\frac{6}{10}-\frac{2}{10}) \\
&= -\frac{4}{10} \\
&= -\frac{2}{5}
\end{align}\)
分数の絶対値の比較についてはこちらを見てください。
分数同士の比較
①分母が同じ場合：分子が大きい方
（例 \(\frac{1}{4} < \frac{3}{4}\)）
②分子が同じ場合：分母が小さい方
（例 \(\frac{1}{4} < \frac{1}{3}\)）
③分母も分子も異なる場合：分母を合わせて①のやり方で考える（通分）
例 \(\frac{1}{6} < \frac{1}{4}\)
通分
\(\frac{1}{6} = \frac{2}{12}\)
\(\frac{1}{4} = \frac{3}{12}\)
分数の通分、そして約分まで忘れずに！
まとめ（基本は数直線！パターン化を目指そう！）
いかがでしたか？
とりあえず、パターン化を覚えられるように頑張ろう！
パターン化が決まっていますが、よくわからない場合は数直線に立ち返りましょう！
そして、またパターン化を覚える
そのサイクルで頑張ってみてください。
この先は他の計算になったり、3つ以上の計算になりますが、この基本は忘れずにいてください！
忘れたら戻ってやり直しましょう。
数学は積み上げの教科です。
覚えてからは早いのでそれまで辛抱です！
それでは！
コメント