こんにちは!ベーです。
今回は、正負の数の大小関係について学んでいきます!
具体的にいうと、不等号(\(<, >, ≦, ≧\))を使った問題ですね。
落とし穴も多く、最初は時間がかかってしまうかもしれませんが、繰り返せばいずれ慣れていきます。
・不等号の意味を確認したい人
・負の数が入った不等号の問題をどうしても間違えてしまう人
・小数と分数の比較を確認したい人
ぜひチェックしてください!
問題練習もありますので、一つずつ丁寧に取り組みましょう!
不等号
不等号は最初に書いた4つを意味します。

僕が授業をしていたときは、
ひらがなの「く」とか「逆く」や
ジェスチャーで表す人が大半だったね(笑)
よほどのことがないと正式な読み方を使わないんでしょうね。
ただ、読み方があるのでそちらも合わせて紹介します。
不等号の読み方と意味
不等号の種類
\(>\)(大(だい)なり)・・・左の方が大きい
\(≧\)(大なりイコール、以上)・・・左の方が大きいまたは等しい
\(<\)(小なり)・・・左の方が小さい
\(≦\)(小なりイコール、以下)・・・左の方が小さいまたは等しい
どちらが大きいかは
大きい方が口が開いていると見ればいいです。

小学校で扱っていると思うけど、忘れている人は、再度復習しようね!
負の数の大小関係
今回で一番間違えやすいポイントです。
負の数の大きさ比べをしてみましょう!
例
次の数の大小を不等号を使って表しなさい。
\(-3\)と\(-5\)

小さい方を答えればいいんだよね!
\(-3\)!

残念!不正解!

え!何が違うのさ!3の方が小さいでしょ!
このやりとりは、演習をさせてる中で本当にたくさんありました。。
負の数を扱うにあたっての最初の壁ですね。
この壁の対策としては、

それは「絶対値が小さい方」だね。
数直線を使って見てみよう。
数直線で確認してみましょう。
数直線上で小さい数は右と左のどちら側に点があるでしょうか?

それはもちろん、左側だよ。
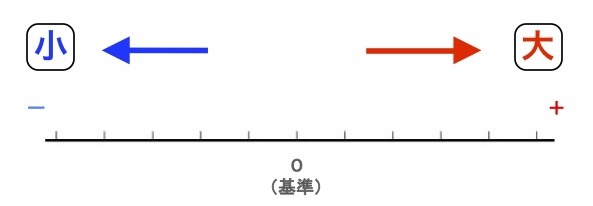
ということは、
\(-3\)と\(-5\)を数直線で当てはめると、、、
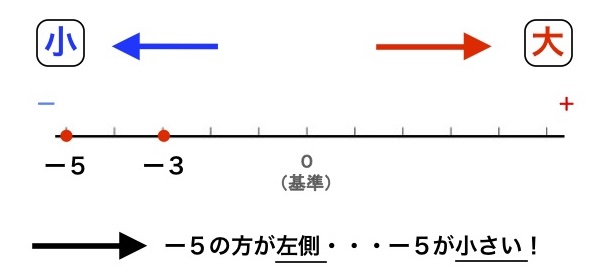

あ、\(-5\)の方が小さいね!
そうです。負の数同士の大小関係は
・絶対値が大きい方が小さい
です!

大きい?小さい?
改めて整理しましょう。
負の数同士の大小関係
絶対値が大きい方(数字が大きい方)
が小さい。
例 \(-3\)と\(-5\)
絶対値(数字)が大きい方は \(-5\)
なので、小さい数は \(-5\)
大小関係は
\(-3 > -5\)
注意したいのはこれは負の数同士の時のみです!
正の数同士や正の数と負の数の場合は違いますので問題文の読み間違いに注意してください!

テストでやらかしそー
注意して問題を解かないと、、
大小関係 練習問題
正負の数の大小関係
次の各組の数の大小を不等号を使って表しなさい。
(1) \(0, +5, -1\)
(2) \(-2, -6\)
(3) \(-0.2, -\frac{1}{4}\)
正の数と負の数の比較はシンプルですね!
0が入っても同じです。
負の数同士の問題はポイントに注意しましょう!
絶対値(数字)が大きい方が小さいです!
大小関係 解答
(1) \(-1 < 0 < +5\)
(2) \(-6 < -2\)
(3) \(-\frac{1}{4} < -0.2\)
(1) 負の数、0、正の数の順で大きくなってますよね。
不安であれば数直線を確認しましょう。
(2) 負の数同士の比較です。
絶対値(数字)が大きいのは\(-6\)(絶対値は\(6\))なので
小さいのは\(-6\)ですね。
(3)負の数同士の比較です。
絶対値(数字)が大きい方を調べればいいんですが、小数と分数の比較ですね。
この時は、
・分数を小数にする
・小数を分数にする
のどちらかにして、同じ種類で比較しましょう。
⚪︎\(-\frac{1}{4}\)を小数にする
小数にするには、割り算をすればいいですね。
(分子)\(\div\)(分母)なので
\(1 \div 4 = 0.25\)
\(0.2\)と\(0.25\)では大きいのは\(0.25\)
なので小さいのは\(-0.25\)なのですが、、

じゃあ答えは\(-0.25 < -0.2\)だね!

ちょっと待って!問題の式を確認して!
問題文は\(-\frac{1}{4}\)なので、小さいのは\(-\frac{1}{4}\)として解答をしましょう!

この間違いは採点してて本当に多くあったよ。
勿体ないな、、って思いながら×にしてたよ。。
間違えても\(-0.25\)としないように!!!
⚪︎\(0.2\)を分数にする
分数にするには、まず\(\frac{}{10}\)の形で表しましょう。
分数の表し方
\(0.1 = \frac{1}{10}\)
\(0.01 = \frac{1}{100}\)
\(0.001 = \frac{1}{1000}\)
桁数に応じて分母を増やします。
これらを元に\(0.2\)を分数にすると、
\(0.2 = \frac{2}{10}\)
約分すると
\(\frac{2}{10} = \frac{1}{5}\)
なので、\(\frac{1}{4}\)と比較すると大きいのは\(\frac{1}{4}\)ですね
分数同士の比較(大きいのは)
①分母が同じ場合:分子が大きい方
(例 \(\frac{1}{4} < \frac{3}{4}\))
②分子が同じ場合:分母が小さい方
(例 \(\frac{1}{4} < \frac{1}{3}\))
③分母も分子も異なる場合:分母を合わせて①のやり方で考える(通分)
例 \(\frac{1}{6} < \frac{1}{4}\)
通分
\(\frac{1}{6} = \frac{2}{12}\)
\(\frac{1}{4} = \frac{3}{12}\)
もちろん、問題文は\(0.2\)なので、解答は\(-0.2 < -\frac{1}{4}\)です。
\(-\frac{1}{5} < -\frac{1}{4}\)としないように!
まとめ(基本は数直線!)
◎大小関係
・正の数と負の数の比較
➡︎ 正の数が大きい!
・負の数同士の比較
➡︎絶対値が大きい方が小さい!
・分数や小数がある比較
➡︎問題文の数に戻すことを忘れずに!

絶対値は直感的にわかる気がするな
ただ、大小関係は落とし穴が多そう

絶対値は数字の部分を意識するだけ!
大小関係はパターンによって分かれているから引っかかりやすいかもね。。
大小関係はさまざま注意することがあって、ミスが起きそうですね。
ただ、基本は数直線です。
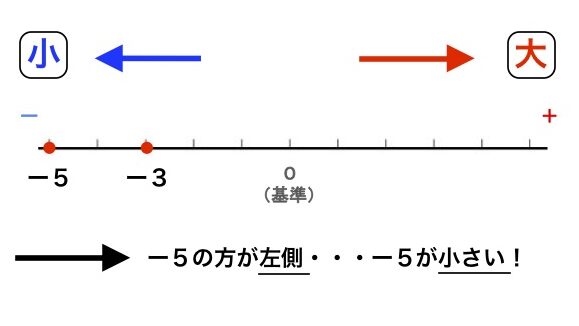
この図にあった通り、左側が小さく、右側が大きいです!
もし迷ったら、数直線をかいて点を取ってみてください。
そして、慣れてきたら比較方法を試して素早く解けるように工夫をしてみましょう。
最初は分からなくても遅くても問題ありません。
ややこしい事が増えていきますが、一つずつ丁寧にこなして、自分のものにしていきましょう。
それでは!


コメント