こんにちは！ベーです。
今回は、正負の数の絶対値について学んでいきます！
絶対値って正負の数と何が違うの？
新しい数習いすぎて訳わかんないよ（泣）
そうですね。絶対値は正負の数と区別しにくいところがあります。
ですが！これらは数直線を理解できれば問題ありません！
正直いうと、絶対値を求める問題はとても簡単に解けます。
ただ、絶対値の応用になると実は単純にいきません。
これは絶対値の意味や求め方を理解すれば、敵ではありません。
最後にコラムとして載せていますので、ぜひご覧ください！
正負の数について理解した状態で取り組んで欲しいので、ビミョーな人は以下を見て確認してください！
絶対値
絶対値の意味は以下の通りです。
絶対値・・・数直線上で、ある数に対応する点と原点との距離
簡単に言えば、距離を表すと思えばいいよ！
正負の数について考えた際に以下の図が出ていたことは覚えているでしょうか？
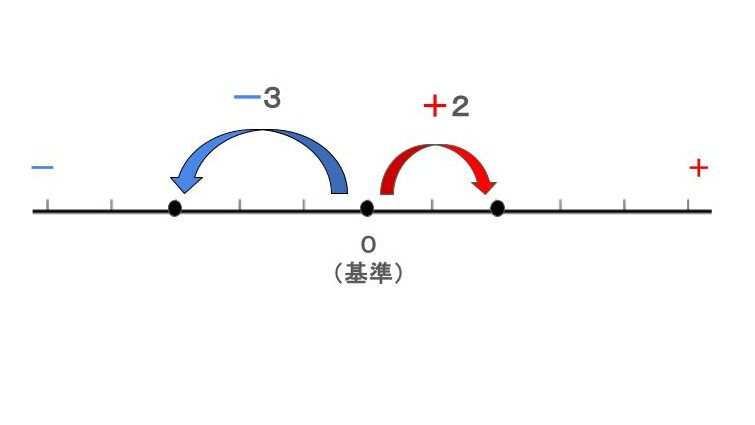
これって正負の数が
・０から左右のどちらかに動いたか
・０からいくつ動いたか
で決まるんだよね。
そうだね。
絶対値はこの中の、いくつ動いたかを表す数なんだ。
絶対値は正負の数のように、＋やーを無視して数字だけ書きます！
ですので、＋を外した正の数とも見ることができます。
（これがややこしいですね、、）
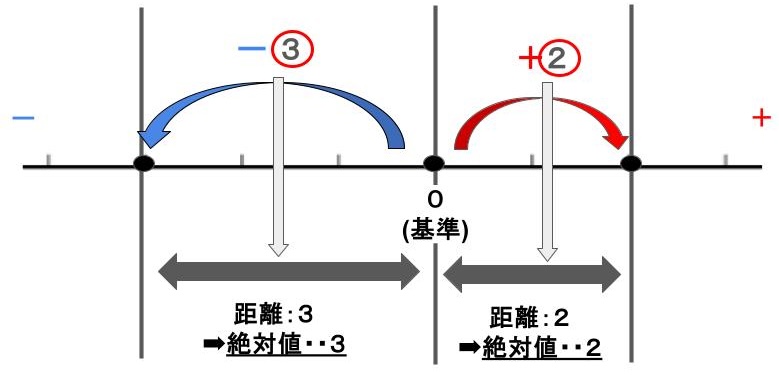
そしたら
絶対値を答えなさい
→＋やーを外して答えなさい
って思ってやればいいね！
今回は正直それでオッケーだね。
ただ、、、
絶対値はこれだけで問題ないのですが、
応用問題や高校に進むと扱いがちょっと面倒になります。
それについては最後にコラムとして載せていますのでぜひご覧ください。
絶対値とは、
・数直線上の距離
・正負の数の符号（＋やー）を外したもの
・符号を外した正の数と同じ見た目なので
正の数として見ることができる
絶対値 練習問題
問１ 絶対値を答える
次の数の絶対値を答えなさい。
(1) ー10
(2) ＋2.5
(3) ０
先ほど伝えた解答方法に沿っていけば問題ないですね。
0のは符号がつかないので？？と思いそうですが、、
外すものがないなら何もしなきゃいいですね！
絶対値 解答
問１
(1) 10
(2) 2.5
(3) 0
符号を外す、外すものがないならそのままでいいですね！
まとめ（絶対値は距離！）
いかがでしたか？
問題としては、符号を外すだけなので簡単に見えたかもしれませんが、
実際は、「距離を表しているんだ」というように
意味を理解して進めていくようにしてください！
やり方だけの暗記は、先で苦労してしまうのでオススメできません。
時間がないかもしれませんが、一つずつ丁寧に理解して解いていきましょう！
それでは！
コラム 絶対値応用
※この内容は正負の数の乗法、文字式の内容を含みます。
そしたら
絶対値を答えなさい
→＋やーを外して答えなさい
ってやればいいね！
先ほどこの考え方がありましたが、絶対値の答え方は以下のように考えられます。
例１ \(+3\)の絶対値
\(+3\)は正の数なのでそのまま符号を外す
答え：\(3\)
例２ \(-3\)の絶対値
\(-3\)は負の数なので\(-\)をつけて正の数にします。
答え：\(-(-3) = 3\)
例２にあるように
⚪︎絶対値の対象になっている数が負の数の場合には\(-\)をつける必要がある
ということです。
この応用が次の問題になります。
問
\(x\)の絶対値を\(x\)が取る値によって分類しなさい。
絶対値の対象になっている数が、負の数だったら\(-\)をつけます。
解答
・\(x\)が負の数の時（\(x < 0\)）
➡︎ \(-x\)
・\(x\)が\(0\)または正の数の時（\(0 ≦
x\)）
➡︎ \(x\)
「絶対値なのに『\(-\)』がついとるやんけー」
となりそうですが、
絶対値の求め方を考えれば問題ないですね。
入試対策や応用問題で出てくる可能性がありますのでもし出たら注意して解きましょう！
コメント